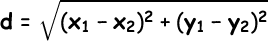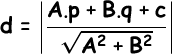Linda Kurnia Lany: Agustus 2013

Selasa, 06 Agustus 2013

rumus cepat dan keceee

Strategi mengerjakan soal matematika dengan rumus cepat sangat efektif terutama dalam menyelesaikan soal Ujian Nasional SD, SMP , SMA maupun SNMPTN. Dengan menggunakan rumus biasa ataupun jadul bisa menghabiskan waktu bermenit-menit tapi dengan menggunakan rumus cepat satu soal matematika bisa dikerjakan dalam hitungan detik.

Model dan variasi soal ujian matematika yang itu-itu saja menjadikan peluang siswa menggunakan trik pengerjaan yang tidak semestinya alias menggunakan jalan pintas dengan rumus cepat (instan).

Contoh rumus cepat matematika banyak sekali yang sering (hampir selalu) berguna ketika UN, SPMB, UMPTN di antaranya adalah rumus tentang deret aritmetika.

Contoh soal:

Jumlah n suku pertama dari suatu deret adalah Sn = 3n² + n. Maka suku ke-11 dari deret tersebut adalah…

Tentu ada banyak cara untuk menyelesaikan soal ini.

Cara pertama, tentukan dulu rumus Un kemudian hitung U11. Cara ini cukup panjang dan memakan banyak waktu serta pikiran sehingga menguras banyak energi. Tetapi bagus Anda coba untuk meningkatkan keterampilan dan pemahaman konsep deret. Rumus Un dapat kita peroleh dari selisih Sn – S(n-1)dan seterusnya. Saya yakin semua sudah bisa

Cara kedua, sedikit lebih cerdik dari cara pertama. Kita tidak perlu menentukan rumus Un. Karena kita memang tidak ditanya rumus tersebut. Kita langsung menghitung U11
S11 – S10 = U11
[3(11²) + 11] – [3(10²) + 10]
= 3.121 – 3.100 + 11 – 10
= 64

Persamaan Kuadrat

contoh soal :

1. UMPTN 1991

Persamaan kuadrat yang akar-akarnya kebalikan dari akar-akar persamaan 2x²-3x +5 = 0 adalah..

A. 2x² -5x +3 = 0

B. 2x² +3x +5 = 0

C. 3x² -2x +5 = 0

D. 3x² -5x +2 = 0

E. 5x² -3x +2 = 0

METODE CERDAS/SMART:

Persamaan kuadrat yang akar-akarnya kebalikan dari akar-akar ax²+bx +c = 0 Adalah : cx² +bx +a = 0 (Kunci : posisi a dan c di tukar )

Jawab:

5x² -3x +2 = 0 (E)

Untuk mengetahui Strategi Cerdas yang lain pada Bab Persamaan Kuadrat silahkan download rumus cepat persamaan kuadrat komplit

Logaritma

contoh soal:

UMPTN 1997

Jumlah dari penyelesaian persamaan : ²log²x +5²log x +6 = 0 sama dengan….

¼
¾
1/8
3/8
-5/8

Jawab:

Pembahasan smart/cara cepat

ingat!

^alog f(x) = p maka :

f(x) = a^p

^maka:

²log²x +5²log x +6 = 0
(²log x +2)(²log +3) =0
²log x = -2 atau ²log x = -3
x = 2^-2 = ¼ atau x = 2^-3 = 1/8

Maka : x1 + x2 = ¼ + 1/8 = 3/8

Untuk mengetahui Strategi Cerdas yang lain pada Bab Logaritma slahkan download rumus cepat logaritma komplit

Peluang

contoh soal :

UMPTN 1998

Seorang murid diminta mengerjakan 5 dari 7 soal ulangan, tapi soal nomor 1 dan 2 harus dikerjakan. Banyaknya pilihan yang dapat diambil murid tersebut adalah….

Penyelesaian cara cepat :

No. 1 dan 2 harus dikerjakan, maka sisa nomor yang dipilih : 3 ,4 ,5 ,6 ,7

Dipilih 3 soal lagi,maka :

C⁵₃ = (5.4) /(2.1) = 10

Untuk mengetahui Strategi Cerdas yang lain pada Bab PELUANG slahkan download rumus cepat PELUANG komplit

Invers

Tentukan invers dari :

F(x) = (2x + 2)² – 5

Cara biasa :

F(x) = y = (2x + 2)² – 5

y + 5 = (2x + 2)²

(y + 5)^1/2 = 2x + 2

(y + 5)^1/2 – 2 = 2x

[(y +5)^1/2 - 2]/2 = x

Jadi F’(x) = [(x + 5)^1/2 - 2]/2

Cara Cerdas :

Lihat : (2x + 2)² –5

pada fungsi tersebut pertama x dikalikan 2 kemudian ditambah 2 lalu dipangkatkan 2 kemudian dikurang 5

Untuk mendapatkan inversnya sekarang langkahnya di balik / dari belakang dan operasinya tiap langkah diubah dengan menggunakan inversnya

hasilnya : x ditambah 5 kemudian dipangkat 1/2 lalu dikurang 2 kemudian dibagi 2

so jawabannya : F’(x) = [(x + 5)^1/2 - 2]/2

kalau anda sudah terbiasa saya yakin dalam hitungan detik anda sudah dapat menyelesaikannya dengan benar. untuk soal yang lain pun dengan cara yang sama.

selamat mencoba!!!

Tidak Semua trik cepat dapat di tuliskan di halaman ini, karena keterbatasan halaman serta format penulisan di blog yang kurang mendukung untuk penggunaan simbol-simbol matematika.

Untuk Bab- bab Yang Lain silahkan download di bawah ini :

Senin, 05 Agustus 2013

Persamaan Lingkaran

by mediabelajaronline.blogspot.com

Persamaan Lingkaran :

Pusat = ( a,b)
Jari-jari = r

Jika bentuk yang dalam kurung dikuadratkan maka.....

Pusat (P) dan jari-jari r :

Catatan :
dalam menentukan persamaan lingkaran sering digunakan rumus

1. Jarak titik (x₁,_y1) ke titik (_x2,_y2) adalah d maka :

2. Jarak titik (p,q) ke garis Ax + By + C = 0 adalah d maka :

Hubungan Lingkaran dengan Garis Lurus

Persamaan garis y = px + q disubtitusikan ke dalam persamaan lingkaran untuk menggantikan variabel y sehingga diperoleh persamaan kuadrat ax² + bx + c = 0

Hubungan keduanya dapat ditentukan dengan nilai diskriminannya ( D )

Jika D > 0 → Persamaan garis berpotongan dengan lingkaran di dua titik
Jika D = 0 → Persamaan garis bersinggungan dengan lingkaran
Jika D < 0 → Persamaan raris tidak berpotongan/bersinggungan dengan lingkaran

Persamaan Garis Singgung Lingkaran

1. Lingkaran ( x - a )² + ( y - b )² = r² dengan gradien garis singgung m

2. Persamaan garis singgung di titik (p,q) pada :
a. Lingkaran ( x - a )² + ( y - b )² = r² adalah :

b. Lingkaran x² + y² + Ax + By + C = 0 adalah :

Sketsa Persamaan Lingkaran

Seringkali untuk menyelesaikan suatu persamaan lingkaran diperlukan kemampuan untuk menggambarkan sketsanya sehinggga gambaran mengenai persamaan lingkaran tersebut menjadi lebih jelas dan mudah difahami.

Coba perhatikan penyelesaian soal - soal persamaan lingkaran di bawah ini :

Tentukan persamaan lingkaran yang :

a. berpusat di (2,-3) dan melalui titik (5,7)

b. berpusat di (10,5) dan menyinggung sumbu y

c. berpusat di (-1,-2) dan menyinggung garis 4x + 3y + 5 = 0

d. pusatnya pada garis y = x - 3 dan menyinggung sumbu x di titik (5,0)

Jawab :

Jari-jari lingkaran = r = jarak titik (2,-3) dengan titik (5,7)

sehingga persamaan lingkarannya :

( x - 2 )² + ( y + 3 )² = 109

b.

karena menyinggung sumbu y maka jari-jarinya ( r) = absis (x) pusat lingkarannya = 10

sehingga persamaan lingkarannya :

( x - 10 )² + ( y - 5 )² = 100

c.

r = jarak titik (-1,-2 ) ke garis 4x + 3y + 5 = 0

sehingga persamaan lingkarannya :

( x + 1 )² + ( y + 2 )² = 1

d.

dari sketsa terlihat bahwa titik X pusatnya = titik singgungnya = 5
kemudian dengan memasukkan nilai X = 5 ke persamaan garis y = x - 3 diperoleh nilai Y pusatnya

y = 5 - x = 5 - 3 = 2

sehingga titik pusatnya = (5,2)

karena menyinggung sumbu x maka jari-jarinya ( r) = ordinat (y) pusat lingkarannya = 2

sehingga persamaan lingkarannya :

( x - 5 )² + ( y - 2 )² = 4

Persamaan Lingkaran

by http://id.wikibooks.org

Persamaan lingkaran

Lingkaran dengan jari-jari r=1, berpusat di (a,b)=(1,2 , 0,5)

Persamaan Lingkaran adalah tempat kedudukan titik-titik (x,y) yang berjarak sama terhadap satu titik tertentu.
Persamaan umum lingkaran adalah:

$\boldsymbol (x-x_p)^2 + (y-y_p)^2 = r^2$

Penting! Bagi siswa SMA, Anda diharuskan hafal rumus persamaan umum lingkaran karena keluar dalam ujian nasional!

Mencari jarak antara 2 titik A (x₁,y₁) dan B (x₂,y₂):

$r = \sqrt { (x_1-x_2)^2 + (y_2-y_1)^2}$

Mencari jarak antara titik A (x₁,y₁) dan garis Ax+By+C=0 :

$d = \left\vert \frac {Ax_1+By_1+C}{\sqrt {A^2+B^2}} \right\vert$

Mencari jari-jari (r) jika diketahui persamaan lingkaran $x^2 + y^2 + Ax + By + C=0$ :

$r= \sqrt {\frac {1}{4}A^2 + \frac {1}{4}B^2 - C}$

Contoh 1:
Tentukan persamaan lingkaran yang berpusat di A(2,7) dan melalui B(5,3)!
Jawab:

$r= \sqrt { (5-2)^2 + (3-7)^2}$

$r= \sqrt {25}$

$r= 5$

$\boldsymbol (x-x_p)^2 + (y-y_p)^2 = r^2$

$\boldsymbol (x-2)^2 + (y-7)^2 = 25$

$x^2+y^2-4x-14y+28=0$

Contoh 2:
Tentukan persamaan lingkaran yang berpusat di puncak parabola $y=x^2-2x+5$ dan menyinggung garis $3x+4y+5=0$ !
Jawab:

$y=x^2-2x+5$

$x_p = - \frac {b}{2a} = - (\frac {-2}{2})= 1$

$y_p = 1^2 - 2 \times 1 + 5 = 4$

maka berarti titik pusatnya berada pada koordinat (1,4).

$3x+4y+5=0$

$A=3, B=4, C=5$

$d = r = \left\vert \frac {Ax_1+By_1+C}{\sqrt {A^2+B^2}} \right\vert$

$d = r = \left\vert \frac {3 \times 1 + 4 \times 4 + 5}{\sqrt {3^2+4^2}} \right\vert$

$d = r = \frac {24}{5}$

$\boldsymbol (x-x_p)^2 + (y-y_p)^2 = r^2$

$\boldsymbol (x-1)^2 + (y-4)^2 = \frac {576}{25}$

$x^2+y^2-2x-8y+17 - \frac {576}{25}=0$

$25x^2+ 25y^2 - 50x - 200y - 151=0$

Kedudukan garis terhadap lingkaran

Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax²+bx+c=0.
Lihat diskriminannya: $D=b^2-4 ac$
Jika

D<0, berarti garis berada di luar lingkaran (tidak memotong lingkaran)
D=0, berarti garis menyinggung lingkaran
D>0, berarti garis memotong lingkaran di 2 titik berbeda.

Contoh 1:

Tentukan posisi garis:
- $y= x+10$ terhadap lingkaran $x^2+y^2= 9$

Jawab:

$x^2 + (x+10)^2=9$

$x^2+ (x^2+20x+100)-9=0$

$2x^2 +20x+91=0$

$D=b^2-4 ac$

$D=20^2- 4\times 91 \times 2$

$D= 400-728= -328$

Karena $D<0$ , maka garis berada di luar lingkaran.
Contoh 2:

Tentukan p agar garis $y= -x+p$ terletak di luar lingkaran $x^2+y^2-2x-4y+3=0$ !

Jawab:

$x^2+ (-x+p)^2 - 2x- 4(-x+p)+ 3=0$

$2x^2 - 2px + p^2 - 2x + 4x -4p + 3=0$

$2x^2 + (2-2p)x + p^2 -4p + 3=0$

syarat: $D<0$

$(2-2p)^2-4(2)(p^2-4p+3)<0$

$4p^2-8p+4-8p^2+32p-24<0$

$-4p^2+24p-20<0$

$-4(p^2-6p+5)<0$

$-4(p-5)(p-1)<0$

$p=5$ atau $p=1$

Gambar dengan garis bilangan untuk pertidaksamaan diatas, maka akan didapatkan nilai p: $p<1$ atau $p>5$

Persamaan garis singgung lingkaran

Perhatian! Persamaan garis singgung lingkaran merupakan salah satu bahan yang diujikan dalam ujian nasional.

Persamaan garis singgung untuk suatu titik (x₁,y₁) yang terletak pada lingkaran

Jika persamaan lingkaran $x^2+y^2=r^2$ , maka persamaan garis singgungnya:

$x_1x + y_1y = r^2$

Jika persamaan lingkaran $(x-x_p)^2+ (y-y_p)^2=r^2$ , maka persamaan garis singgungnya:

$(x_1-x_p)(x-x_p) + (y_1-y_p)(y-y_p) = r^2$

Jika persamaan lingkaran berbentuk $x^2 + y^2 + Ax + By + C =0$ , maka persamaan garis singgungnya:

$x_1x + y_1y + \frac {1}{2} A(x+x_1) + \frac {1}{2} B(y+y_1)+C=0$

Persamaan lingkaran $x^2 + y^2 + Ax + By + C =0$ dapat juga diubah menjadi $(x-x_p)^2+ (y-y_p)^2=r^2$ dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.