PROGRAM LINEAR
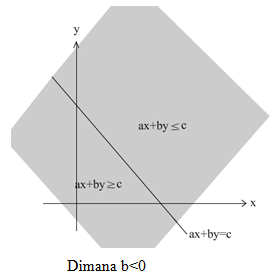
c. Garis Yang Membagi Bidang Menjadi Dua Bagian
Program linier untuk dua variabel dapat ditulis dengan :
Maksimum , dengan batasan :
, dengan batasan : 
, Atau
Minimun , dengan batasan :
, dengan batasan : 
Persoalan yang ada adalah bagaimana menentukan nilai x dan y yang terdapat pada kendala yang membuat fungsi tujuan f (x,y) menjadi optimum (maksimum/minimum).
Contoh :
Tentukan nilai maksimum : , dengan batasan :
, dengan batasan : 
Jawab :
Himpunan Penyelesaian dari sistem Pertidaksamaan : adalah daerah yang diarsir pada grafik dibawah ini :
adalah daerah yang diarsir pada grafik dibawah ini :

Titik-titik ekstrim dari himpunan penyelesaian (HP) adalah :
O (0,0); A (2,0); C (0,2) dan
Titik A merupakan titik potong garis 3x + y = 6 dengan sumbu x, yaitu:
y = 0 -->
Titik B merupakan titik potong garis 3x + y = 6, dengan garis x + 2y = 4, yaitu :

Titik O merupakan titik potong garis x = 0 dengan y = 0
Nilai f (x,y ) = 4x + y pada setiap titik ekstrim adalah :
1. Menentukan Nilai Optimum
Hal yang harus diperhatikan dalam menyelesaikan soal dengan program linier :
a. Tentukan model matematikanya
b. Gambar grafik dari model tersebut
c. Tentukan daerah himpunan penyelesaian
d. Tentukan titik-titik verteks (pojok)
2. Persamaan Garis
a. Persamaan dengan gradien m melalui P (x1, y1) adalah y - y1 = m (x - x1)
b. Persamaan garis yang melalui dua titik P (x1, y1) dan Q (x2, y2) adalah :
c. Garis Yang Membagi Bidang Menjadi Dua Bagian
3. Program Linear
Di dalam program linier kita akan menemukan sebuah fungsi linier yang disebut fungsi tujuan atau
fungsi objektif dan sebuah sistem pertidaksamaan linier yang disebut kendala atau batasan.Program linier untuk dua variabel dapat ditulis dengan :
Maksimum
 , dengan batasan :
, dengan batasan : 
, Atau
Minimun
 , dengan batasan :
, dengan batasan : 
Persoalan yang ada adalah bagaimana menentukan nilai x dan y yang terdapat pada kendala yang membuat fungsi tujuan f (x,y) menjadi optimum (maksimum/minimum).
Contoh :
Tentukan nilai maksimum :
 , dengan batasan :
, dengan batasan : 
Jawab :
Himpunan Penyelesaian dari sistem Pertidaksamaan :
 adalah daerah yang diarsir pada grafik dibawah ini :
adalah daerah yang diarsir pada grafik dibawah ini : 
Titik-titik ekstrim dari himpunan penyelesaian (HP) adalah :
O (0,0); A (2,0); C (0,2) dan

Titik A merupakan titik potong garis 3x + y = 6 dengan sumbu x, yaitu:
y = 0 -->
x = 2
Jadi A (2,0)
Titik C merupakan titik potong garis x + 2y = 4 dengan sumbu y, yaitu :
y = 2
Jadi C (0,2)

Titik O merupakan titik potong garis x = 0 dengan y = 0
Nilai f (x,y ) = 4x + y pada setiap titik ekstrim adalah :
f (o) = f (0,0) = 4 (0) + 0 = 0
f (A) = f (2,0) = 4 (2) + 0 = 8
f (C) = f (0,2) = 4 (0) + 2 = 2
Nilai f (x, y) paling besar adalah 8, yang diperoleh pada titik ekstrim A (2,0)